Vehicle Speed and Mortality Rates
Has anyone noticed the new 20mph speed limits cropping up in town centres? What a drag eh?! Well, it's still a lot faster than walking, cycling, or even a horse and cart. But never mind that, it's annoying! Actually there's some reasonably interesting maths that goes into explaining the choice of speed limits in highly pedestrianised areas of the UK. You'll notice, if you ever drive down an English country lane, that the speed limit there is often around 60mph, which realistically you'd only attempt on those roads if you're either a very very good driver, or just plain suicidal. So why is on a nice wide, straight road which you could comfortably cruise at 45mph, has some half-wit set the speed limit at 30mph or even 20mph? The cheek!
The Physics
The maths behind this revolves around two equations. First of all, the equation for kinetic (i.e. moving) energy, this is given by: Ke = 1/2 m v^2 I.e. it is a half the mass times the velocity squared. And another one to do with work done (i.e. how much energy is consumed): WD = F x Which is just force times distance over which the force is applied. These two equations are pretty simple to understand. For the first one just think about which has more moving energy - a heavy object moving very fast, or a light object moving very slowly? Obviously the first one. As for work done, would you rather apply a large force (i.e. push hard) over a large distance, or a push lightly on something for a small distance? I know which I'd choose!
A Reasonable Assumption
We need to make a reasonable assumption, and that is all the work done by the brakes takes off the same amount of kinetic energy. In truth probably some kinetic energy is lost through friction and wind resistance, but by far the biggest factor is the brakes so we'll just ignore the other things to make things simpler.
The Maths
Knowing this, we can plot a graph of how much the speed will decrease after applying the brakes over a certain distance. The kinetic energy before braking is 1/2 mv^2. Let's call this K. To work out how much speed it loses we know it loses Fx amount of energy. So it's new kinetic energy is K - Fx = 1/2 mv^2. Rearranging v in terms of x gives: v = (2/m (K - Fx))^0.5 If we assume a car has constant braking force, then we can plot how the speed changes over distance.
Too Much?
To be honest you can skip the maths section and just jump straight to this bit. The important thing is the shape of the curve you get of speed over distance. The key feature of it is that the speed actually reduces quite slowly at first, and only in the last bit does it all go down:
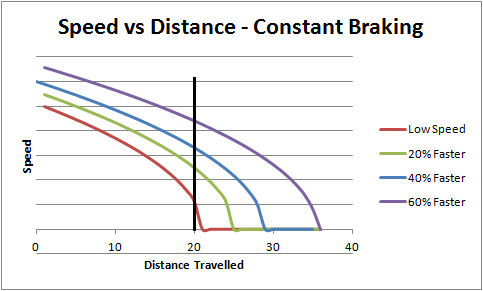
The black vertical line is where the pedestrian could be, 20m from where the driver started braking. Notice how at the lower starting speed (the red line), the pedestrian only gets hit at a speed of one unit. Increasing the initial speed by just 20% more than doubles the final speed the pedestrian gets hit at. At just 60% faster, the final speed is over 4X what the slower speed is.
The Conclusion
Apparently the statistics are something like this: Collisions involving cars that were going at 30mph have an 80% mortality rate. Collisions involving cars that were going at 20mph have a 20% mortality rate. (These may not be 100% accurate as it's only from memory but it's something like that).
(Published on 3 Aug 2017)