
I'm making a big assumption here, but as a mathematician I've calculated that most people either don't like maths or weren't any good at it at school; so I've got a very good chance that the person reading this is not great at maths, and a pretty decent chance they even consider themselves to be incompetent at it. I've recently developed a theory as to how that state of affairs has come to be. And to illustrate it, I'm going to introduce an entirely new subject I've developed, called complexology. It is a very important subject that everyone should learn, you'll need it in the world of work and in your career, and there'll be some pretty difficult exams on it that you'll need to study for and pass before you can do anything else in life. Basically, first of all you take something called a zag. These zags have different symbols, like so: '#+%&*(
The rules are as follows:
##% = *&
@ = #**
^%^ === @@#
and so on.
Ok time for your first test:
If I take the following zags, and imply them over a k-plane, what is the resulting fido-metric? The answer is of course &. I won't bore you with the proof of such a trivial example so let's move on to chapter two.

Ok I think you get the idea. See the great problem with maths, and also it's greatest asset, is that it is almost entirely symbolic. Let's look at the definition of a symbol: "a thing that represents or stands for something else" However, what I have found is often not made clear enough, is the link between the symbol and the something else. Without that crucial link, the symbols are about as meaningful as the mess that is complexology, and it's about as fun to study as power-sanding your own leg.
What should come first is a study of the something else, and later on we should introduce the symbols as a convenient way to refer to things already looked at and understood. What happens often though is the introduction of the symbols and the rules between them, aaand then a test about those things and move onto the next chapter. So in actual fact nothing has been studied there whatsoever except a bunch of meaningless relationships between meaningless symbols. What a big waste of time.
Let's look at an actual example of real maths. Take a look at the following grid of dots, I have put a certain number of dots there. At this point, I refuse to even name that quantity (although I'm sure you know what it is), to make the point that what is important is NOT the name or label which we give to the quantity, but the actual quantity itself. It's like constantly objectifying women and never getting to know the real person - only thinking about what they look like. So probably for the first time in a long time, maybe even ever, I want to introduce you to this guy:

He is a pretty interesting dude, not least because he can be rearranged in the following way:

See how he (I've just noticed I've defaulted to considering it to be a male here, but whatever) can be put nicely into two neat rows, each row the same size as the previous (and yes I did just use the label two, but I realised this will get very difficult if I refuse to use any names for numbers, which I think illustrates my point that the names are useful when trying to communicate or refer to different mathematical objects). Amazingly though, he can also be arranged like this:

How about that. Fits equally neatly into three rows. But what about 5 rows:

Oh dear. That didn't work did it. Well it's still pretty good going. But why is that, why is it possible to put him into 2, 3, or 4 rows, but not 5? Strange isn't it. What's even stranger, is that if I take just one dot away, and look at the guy that lives next to him, i.e. this guy:
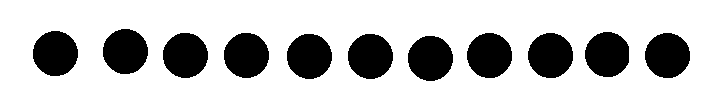
Will only ever fit into one row. Try as you like, it won't go neatly into any equally sized rows other than one. That's pretty crazy isn't it, like how can we take just one dot away and rather than the nice jolly cooperative chap we got before, we're introduced to a stubborn, obnoxious, uncooperative bore? It still baffles me. Yet this rather intriguing problem, which has confounded the greatest minds to ever grace the face of the earth, for centuries, can be quite boringly and inconsequentially be stated in the language of standardly educated mathematics:
"Ahem, listen up everybody. A prime number is a number that can only be divided by one and itself. Ok class, make sure you remember that definition because it's going to be on the next class test. Also you need to know that the following numbers are prime: 2,3,5,7,11." And in my opinion that is why you suck at maths: you've probably never even come close to studying it in the first place. What you think you're not good at isn't even maths at all, it's a paper thin veneer with nothing underneath; masquerading as the bright, vibrant, solid block of wood that it should be.
(Published on 12 Apr 2016)
Richardhowellpeak.com