
In this article here- SKY SPORTS

Mr Balague makes a pretty hasty claim that Ronaldo's days as a goal-scoring machine are behind him. In this article we'll take a closer look at that claim and see if it stacks up to mathematical scrutiny. This is an actual piece of maths I did with a student recently in a statistics lesson. Ok, so first of all, let's get the numbers. To simplify matters we'll just look at league goals over his entire career:
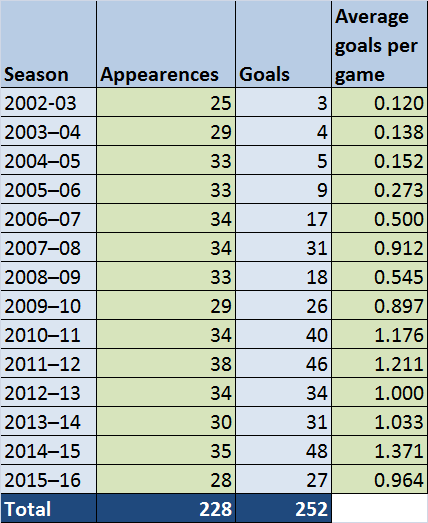
Which if you graph looks like this:
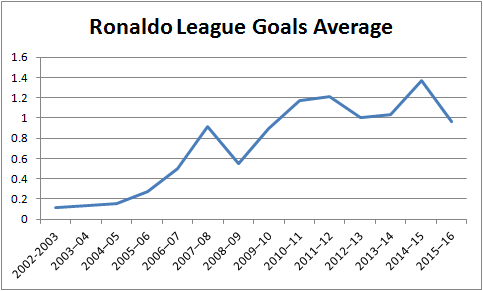
Pretty decent. Now we can see that from 2010 up until 2015, he's been pretty consistent in his goal scoring capabilities. Let's take that then to be the mean rate of goals, which works out to roughly 1.164 goals per game. This is a Poisson distribution, with mean rate of 1.164. We take this to be the null hypothesis. The alternative hypothesis then is that the mean is less than that. Let's do a standard 5% tolerance test. Now let's look at the most recent season gone. In this he's played 28 league games, which means if he was scoring at the mean rate that would be roughly 32 goals we would expect. So to test this we would need to establish what the probability is of him scoring a measly 27 goals is when his supposed average is 32. In mathematical language then, what is P(X <= 27) when X~Po(32).
Since the Poisson tables don't go up to 32, we approximate using a Normal distribution N(32, 32). So, to look this up in the tables we must translate it to the standard Normal distribution, so z = (27 - 32 ) / 32 = -0.16 roughly. Looking that up in the Normal tables gives a probability of 56%. But remember the tables only give us the value for the positive side. As in the diagram below we've essentially worked out the probability it is less than +0.16, which is the orange region, but we want the probability it is less than -0.16, which would be the blue region.
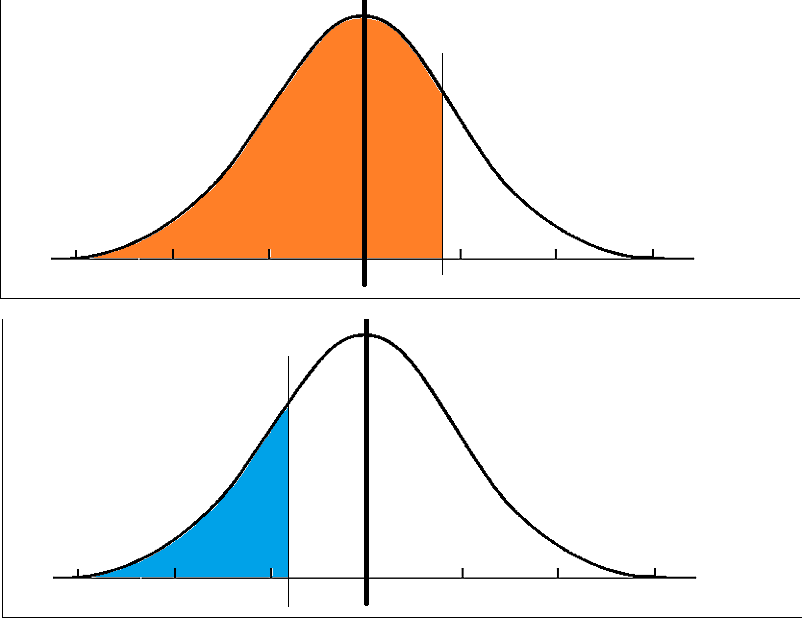
Hopefully it's easy to see that they both add up to one, so we must take the result to be 44%. So what have we established? Well according to the null hypothesis, we would have a 44% chance of obtaining the goal scoring record we have seen of Ronaldo this season. This is well outside the very reasonable 5% tolerance band we allowed ourselves. So under these assumptions, we are forced to conclude that we do not have enough evidence to support Mr. Balague's claim that Ronaldo is past his best. I'm quite disappointed to see such a lack of mathematical rigor in our sports analysis. In the future I'd like to see football pundits backing up their wild claims with some sound statistical analysis, rather than (what has now been made clear) is just his opinion and nothing else. With role models like these football pundits, it's no wonder mathematical standards in schools are dropping at such an alarming rate.
(Published on 15 Mar 2016)
Richardhowellpeak.com